Ad Code
Featured Section
Article épinglé
Formulaire de contact
Consultations de pages
Manoeuvrabilité et observabilité.
Manoeuvrabilité et observabilité sont deux choses très importants liés à l'analyse spatiale État. Il existe de nombreux tests pour vérifier la manoeuvrabilité et obervability et ces tests sont très essentiels lors de la conception d'un système de contrôle à l'aide d'approche de l'espace État.
Manoeuvrabilité vérifie si est État variable est utile ou non. Il vérifie si une variable d'État peut être manipulée pour obtenir la sortie requise. Si une variable d'État n'est pas contrôlable il y a alors aucune signification en sélectionnant pour toute opération. Si une variable d'état particulier est trouvée incontrôlable, alors il est gauche intacte et toute autre variable de l'État qui est contrôlable est sélectionné pour les opérations.
Un système est dit être complètement énoncer contrôlable, s'il est possible de changer le système de n'importe quelle étape initiale X(t0) à n'importe quelle étape requise X(td) à l'aide d'un vecteur de contrôle région. Critère et Maltby de Kalman sont les deux méthodes courantes utilisées pour l'essai de manoeuvrabilité.
Méthode de Gilbert pour vérifier la manoeuvrabilité s'effectue dans deux cas.
1) Lorsque les valeurs d'eigen de la matrice du système sont distinctes.
Dans ce cas, la matrice de système peuvent être diagonalisée et peut être convertie en la forme canonique en donnant une transformation X = MZ. M est la matrice modale dérivée de la matrice de système et z est la matrice variable d'État transformées.
Considérons un système avec le modèle de l'État représenté par les équations
X = AX + BU
Y = CX + DU
Le modèle est transformé en la forme canonique qui suit,
Z = ?Z + B˜U
Y = C˜Z + DU
Où ? = MA¯¹M, B˜ = M¯¹B et C˜ = CM
Le système est complètement énoncer contrôlable si le doesnot de matrice b ont une ligne avec tous les zéros.
2) Les valeurs de Eigen de la matrice du système sont répétées.
Dans cette situation, il est impossible de diagonaliser la matrice de système, et il peut être converti en forme canonique de Jordanie.
Considérons un système avec le modèle de l'État représenté par les équations
X = AX + BU
Y = CX + DU
Le modèle est transformé en la forme canonique de Jordan comme suit,
Z = JZ + ?˜U
Y = C˜Z + DU
Où J = A¯¹M M, B˜ = M¯¹B et C˜ = CM
Le système va être complètement État contrôlable si les éléments de toute ligne de b qui correspondent à la dernière rangée de chaque bloc de Jordan ne sont pas tous les zéro et les lignes correspondant aux autres variables de l'État ne doivent pas avoir tous les zéros.
Rechercher
Categories
Popular Posts
montage amplificateur inverseur
Carte d’extension I2C 64 I/O pour RaspberryPi

schema électrique autoradio

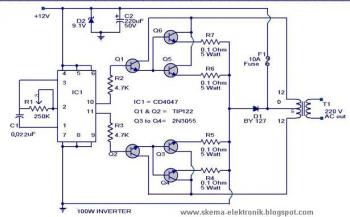
Onduleur 100 Watt 12V DC à 220V AC

Hauteur interrupteur lit








0 Commentaires